Lecture notes.
 

Introduction to Quantitative Genetic Analysis


 This notes serve as a companion to Chapter 5 of  Staistics in Human Genetics. It will guide you work out most of the examples there. Briefly, the contents of the notes are as follows.

Many examples were in SAS. Since currently SAS is unavailable in the institute network it may not be straight forward for non-SAS users. However with the SAS source codes provded in this notes the burden should be relieved quite a lot. We also give some details about MLn, Mx and SAGE.

In the analysis of the  the neuroticism dataset, we used a few packages: SAS in examples 5.1, 5.2, 5.3, 5.9 5.16, 5.18, SPSS in example 5.10, SPSS and MLn in example 5.11, Mx in examples 5.20  and 5.21.

Important !!!

We do not intend to distribute many files. The exceptions are the original data files which are too long to include or too difficult to make, and some Mx programs that are very similar to the codes within this notes. In order to replicate the examples you could take advantage of the copy/cut and paste utility under MS Windows and create your own programs. For example if you want to run the programs for SPSS you could first block the code from web browser (Netscape or Internet Explorer), then select copy from its Edit menu, and finally switch and paste to your SPSS syntax window. From there you block the code and click the execute button to get the result. SPSS can also paste your selections from its own menu. By doing this you would be able to check your choices with ours.
 
The book chapter makes extensive use of Dr Alison MacDonald's data on personality dimension neuroticism. Originally the dataset contains the following variables.

From these, new variables t1, t2 and group were created for the subsequent analyses.

Table 5.1 Cross-tabulation of neuroticism for MZ and DZ twin pairs.

MZ
------------------------------------------------------------------
                                T2
    ----------------------------------------------------------
     1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 ALL
------------------------------------------------------------------
 T1
 3       1  1                                                   2
 4    1  3  4  2                                               10
 5       1  1 12  4                                            18
 6       1  2  6 11  6                                         26
 7          5  5  8  7  6                                      31
 8       1  1  1  4  8  6  3                                   24
 9       1  2  1  5 12  9  8  7                                45
 10         5  3  2  3  8  5  5  4                             35
 11         1  1  4  3  3  9  8  3  5                          37
 12         2  3  3  4  4  6  8  9  4  3                       46
 13      1     2  4  5  4  7  7  6  6  6  3                    51
 14      1     1  3  2  3  1  4  4  9  4 13  5                 50
 15            2  1  2  1  4  4  1  2  5  7  7  3              39
 16            1     1  2  1  2  4  4  5  6  4  4  1           35
 17                  1     1  2  3  2  1  4  6  6  9  1        36
 18            1        1  1  2     1  2  2     5  1  4  1     21
 19      1           1     1  2  1  1  1              2  3  1  14
 20                           1                                 1
 21                                    1                        1
 ALL  1 11 24 41 49 55 47 47 52 35 34 28 35 22 18 11  7  4  1 522
------------------------------------------------------------------

DZ
------------------------------------------------------------
                             T2
    ----------------------------------------------------
     2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 19 ALL
------------------------------------------------------------
 T1
 4       1  1                                             2
 5       1  3  1                                          5
 6       1     2  3                                       6
 7       4  1  4  6  1                                   16
 8    3     3  1  6  4  4                                21
 9       3  4  2  6  2  5  3                             25
 10   1     3  4  2  1  2  2  3                          18
 11      2  1  2  4  4  4  4  2                          23
 12   2  2  1  2  2  4     2  4  1  1                    21
 13      2  1  2  1  1     3  1  3  7  1                 22
 14      1     2  2  5  2  1  2  4  2  1  1              23
 15            1  2  1  1  2  4  5  2     4  2           24
 16   1  3  2  1     1     4  1     2  1  4  3  2        25
 17      1  2     1  1  2  1  1  2  2        3  1  1     18
 18         1     1     3  1  3     1  2  1        1     14
 19                           1     1  1  1        2  1   7
 20                                    1           1      2
 ALL  7 21 23 24 36 25 23 23 22 15 18  7 11  8  3  5  1 272
------------------------------------------------------------

The above  table was created by the following SAS program.

libname x '';
data subset;
  set x.alison;
  where zyg2=2 or zyg2=4;
  if zyg2=2 then do; t1=max(n_1,n_2); t2=min(n_1,n_2); end;
  if zyg2=4 then do; t1=max(n_1,n_2); t2=min(n_1,n_2); end;
  t1=max(n_1,n_2); t2=min(n_1,n_2);
  td=t1-t2;tm=mean(t1,t2);
  group=zyg2/2;
run;
options nocenter ls=120 missing=' ';
title2 'MZ';
proc tabulate data=subset fc=' ----------' noseps f=2. missing;
  class t1 t2;
  where zyg2=2;
  table t1 all, t2 all/rts=5;
  keylabel n=' ';
run;
title2 'DZ';
proc tabulate data=subset fc=' ----------' noseps f=2. missing;
  class t1 t2;
  where zyg2=4;
  table t1 all, t2 all/rts=5;
  keylabel n=' ';
run;

 

Linear Models for continuous twin data using SAS and SPSS 

Example 5.1 One-way ANOVA of neuroticism.

MZ sample

Dependent Variable: N
Source            DF   Sum of Squares   Mean Square   F Value   Pr > F
Model            521         13445.23         25.81      2.72      .00
Error            522          4953.00          9.49
Corrected Total 1043         18398.23

            R-Square             C.V.      Root MSE             N Mean
                 .73            30.04          3.08              10.25
Source            DF         Anova SS   Mean Square   F Value   Pr > F
PAIRID           521         13445.23         25.81      2.72      .00
 

DZ sample

Dependent Variable: N
Source            DF   Sum of Squares   Mean Square   F Value   Pr > F
Model            271          5970.45         22.03      1.48      .00
Error            272          4053.50         14.90
Corrected Total  543         10023.95

            R-Square             C.V.      Root MSE             N Mean
                 .60            37.86          3.86              10.20
Source            DF         Anova SS   Mean Square   F Value   Pr > F
PAIRID           271          5970.45         22.03      1.48      .00
 

The F-test for a genetic contribution.
F=MSW(DZ)/MSW(MZ):=1.5700737619 p=.000006513

The corresponding SAS program is as follows.

data anova;
  set x.alison (keep=pairid n_1 n_2 zyg2);
  where zyg2=2 or zyg2=4;
  keep pairid n nc a c d z twin group wgt;
  group=zyg2/2;wgt=.5;

  n=n_1;nc=n_2;c=nc;
    if group=1 then do; a=nc; d=nc; z=1; end;
    else do;a=nc/2; d=nc/4; z=0;end;
    twin=1;output;
  n=n_2;nc=n_1;c=nc;
    if group=1 then do; a=nc; d=nc; z=1; end;
    else do;a=nc/2; d=nc/4; z=0;end;
  twin=2;output;
run;
title2' test for MZ correlation';
proc anova;
  where group=1;
  class pairid;
  model n=pairid;
run;
title2' test for DZ correlation';
proc anova;
  where group=2;
  class pairid;
  model n=pairid;
run;
 data _null_;
  file print;
  put' Test of genetic contribution';
  f=14.90/9.49;p=1-probf(f,272,522);
  put 'F=MSW(DZ)/MSW(MZ):=' f 'p=' p 10.9;
run;

This part shows testing for heteroscedasticity, intraclass correlation, the SAS codes are self-explanatory.

Example 5.2 The F-test for homoscedasticity.

F=MST(DZ)/MST(MZ):=1.0465195042 p=.268726137

The Z-tests for twin pair correlations are as follows.
MZ z=0.0468542566 p=.142892555
DZ z=0.0038100184 p=.475086731

Example 5.3 The intraclass correlations for MZ and DZ twins.

MZ r=(MSB-MSW)/(MSB+MSW)=0.4623229462
DZ r=(MSB-MSW)/(MSB+MSW)=0.1930679664

The Z-test for equal intraclass correlations is as follows.
z =4.0625533933 p =.000024269

As a measure of the proportion of phenotypic variance accounted for by genetic factors.
Holzinger's H =   0.33368
 

Example 5.9 The MZ:DZ ratio in intraclass correlations.

Ratio of intraclass correlations=2.3946123986
Va=0.3099489195 Vd=0.1523740267 Ve=0.5376770538
Narrow heritability (S.E.)=0.3099489195 0.2360174398
Broad heritability  (S.E.)=0.4623229462 0.0344135556

The SAS program is as follows. It is obvious that you could use QBASIC or  a calculator to perform most of the computations.

data _null_;
  file print;

  put' Test of homoscedasticity';
  f=(10023.95/543)/(18398.23/1043);p=1-probf(f,543,1043);
  put 'F=MST(DZ)/MST(MZ):=' f 'p=' p 10.9;

  put 'Test of twin pair correlation';
  r=0.04682;n=522;
  z=0.5*log((1+r)/(1-r));p=1-probnorm(z/sqrt(1/(n-3)));
  put 'MZ z=' z 'p=' p 10.9;
  r=0.00381;n=272;
  z=0.5*log((1+r)/(1-r));p=1-probnorm(z/sqrt(1/(n-3)));
  put 'DZ z=' z 'p=' p 10.9;

  put 'Intraclass correlation for MZ';
  rm=(25.81-9.49)/(25.81+9.49);
  zm=0.5*log((1+rm)/(1-rm));
  put 'MZ r=(MSB-MSW)/(MSB+MSW)=' rm;
  put 'Intraclass correlation for DZ';
  rd=(22.03-14.90)/(22.03+14.90);
  zd=0.5*log((1+rd)/(1-rd));
  put 'DZ r=(MSB-MSW)/(MSB+MSW)=' rd;
  put 'Test for equal intraclass correlations';
  z=(zm-zd)/(sqrt(1/(522-2)+1/(272-2)));
  p=1-probnorm(z);
  put 'z =' z 'p =' p 10.9;
  h=(rm-rd)/(1-rd);
  put 'Holzinger''s H =' h 10.5;

  rr=rm/rd;
  put 'Ratio of intraclass correlations=' rr;
  va=4*rd-rm;vd=2*rm-4*rd;ve=1-va-vd; hn=va; hb=va+vd;
  put 'Components of genetic variances:';
  put 'Va=' va 'Vd=' vd 'Ve=' ve;

  var_rm=(1-rm**2)**2/522;
  var_rd=(1-rd**2)**2/272;
  var_hn=16*var_rd+var_rm;se_hn=sqrt(var_hn);
  var_hb=var_rm;          se_hb=sqrt(var_hb);

  put 'Narrow heritability (S.E.)=' hn se_hn;
  put 'Broad heritability  (S.E.)=' hb se_hb;

run;

Example 5.10 The linear regression approach for estimating heritability.

The dataset has already been created in example 5.1. Now denote y the mean centered trait value of cotwin we can perform a linear regresssion of  y on A2 and D2 for MZ and DZ twins together using SPSS.

           * * * *  MULTIPLE REGRESSION THROUGH THE ORIGIN  * * * *

Listwise Deletion of Missing Data

Equation Number 1    Dependent Variable..   Y

Block Number  1.  Method:  Enter      A2       D2       Z

Variable(s) Entered on Step Number
   1..    Z
   2..    A2
   3..    D2

Multiple R           .38838
R Square             .15084
Adjusted R Square    .14762
Standard Error      3.90599

Analysis of Variance
                    DF      Sum of Squares      Mean Square
Regression           3          2143.63633        714.54544
Residual           791         12068.07627         15.25673

F =      46.83476       Signif F =  .0000

------------------ Variables in the Equation ------------------

Variable              B        SE B       Beta         T  Sig T

A2              .303566     .224411    .260339     1.353  .1765
D2              .158013     .235236    .129277      .672  .5020
Z               .013347     .170963    .002558      .078  .9378
 

           * * * *  MULTIPLE REGRESSION THROUGH THE ORIGIN  * * * *

Equation Number 1    Dependent Variable..   Y

Block Number  2.  Method:  Backward     Criterion   POUT  .1000
   A2       D2       Z

Variable(s) Removed on Step Number
   4..    Z

Multiple R           .38837
R Square             .15083
Adjusted R Square    .14868
Standard Error      3.90354

Analysis of Variance
                    DF      Sum of Squares      Mean Square
Regression           2          2143.54334       1071.77167
Residual           792         12068.16926         15.23759

F =      70.33736       Signif F =  .0000

------------------ Variables in the Equation ------------------

Variable              B        SE B       Beta         T  Sig T

A2              .303547     .224270    .260323     1.353  .1763
D2              .158051     .235088    .129308      .672  .5016

Equation Number 1    Dependent Variable..   Y

Variable(s) Removed on Step Number
   5..    D2

Multiple R           .38774
R Square             .15034
Adjusted R Square    .14927
Standard Error      3.90219

Analysis of Variance
                    DF      Sum of Squares      Mean Square
Regression           1          2136.65606       2136.65606
Residual           793         12075.05654         15.22706

F =     140.31970       Signif F =  .0000

------------------ Variables in the Equation ------------------

Variable              B        SE B       Beta         T  Sig T

A2              .452124     .038168    .387743    11.846  .0000

The SPSS program should be similar to the following.

* Program for Page 216.
GET
  FILE='C:\iop\lecture\anova.sav'.
EXECUTE .

WEIGHT BY wgt.
REGRESSION
  /MISSING LISTWISE
  /STATISTICS COEFF OUTS R ANOVA
  /CRITERIA=PIN(.05) POUT(.10)
  /ORIGIN
  /DEPENDENT y
  /METHOD=ENTER a2 d2 z /METHOD=BACKWARD a2 d2 z.

Example 5.11 ADE and AE models using SPSS and MLn.

Linear regression under selection with weight=(108+66)/(131+75)=0.845 using SPSS

           * * * *  MULTIPLE REGRESSION THROUGH THE ORIGIN  * * * *

Listwise Deletion of Missing Data

Equation Number 1    Dependent Variable..   Y

Block Number  1.  Method:  Enter      A2       D2

Variable(s) Entered on Step Number
   1..    D2
   2..    A2

Multiple R           .54802
R Square             .30033
Adjusted R Square    .29220
Standard Error      4.15175

Analysis of Variance
                    DF      Sum of Squares      Mean Square
Regression           2          1273.13406        636.56703
Residual           172          2965.97524         17.23703

F =      36.93021       Signif F =  .0000

------------------ Variables in the Equation ------------------

Variable              B        SE B       Beta         T  Sig T

A2              .373490     .304826    .450112     1.225  .2222
D2              .086413     .320181    .099147      .270  .7876
 

          * * * *  MULTIPLE REGRESSION THROUGH THE ORIGIN  * * * *

Equation Number 1    Dependent Variable..   Y

Block Number  2.  Method:  Backward     Criterion   POUT  .1000
   A2       D2

Variable(s) Removed on Step Number
   3..    D2

Multiple R           .54775
R Square             .30003
Adjusted R Square    .29599
Standard Error      4.14061

Analysis of Variance
                    DF      Sum of Squares      Mean Square
Regression           1          1271.87852       1271.87852
Residual           173          2967.23078         17.14469

F =      74.18500       Signif F =  .0000

------------------ Variables in the Equation ------------------

Variable              B        SE B       Beta         T  Sig T

A2              .454511     .052770    .547754     8.613  .0000
 

The SPSS program should look like the following.

* Program for page 218.
GET
  FILE='C:\iop\lecture\anova.sav'.
EXECUTE .
* PROCESS IF is not recognized now.
SELECT IF (nc>15).

COMPUTE wgt_new=0.845.
WEIGHT BY wgt_new.

REGRESSION
  /MISSING LISTWISE
  /STATISTICS COEFF OUTS R ANOVA
  /CRITERIA=PIN(.05) POUT(.10)
  /ORIGIN
  /DEPENDENT y
  /METHOD=ENTER a2 d2 /METHOD=BACKWARD a2 d2.
 

MLn

MLN - Software for N-level analysis.   Tue Feb 17 16:59:22 1998

name c1 'ID' c2 'Y' c3 'wgt' c4 'A2' c5 'D2' c6 'C2' c7 'CONS' c8 'CONSD'
resp 'Y'

note weight==.5
iden 1 'id' 2 'cons'
expl 'cons' 'consd' 'a2' 'd2'
fpar 'cons' 'consd'
setv 1 'cons' 'consd'
sett
EXPLanatory variables in       CONS     CONSD    A2       D2
FPARameters                                      A2       D2
RESPonse variable in           Y
FSDErrors : uncorrected                 RSDErrors : uncorrected
MAXIterations  20   TOLErance     2     METHod is IGLS    BATCh is OFF
IDENtifying codes : 1-ID, 2-CONS

LEVEL 1 RPM
         CONS     CONSD
CONS     1
CONSD    1        1
star

rand
fixe
like
next

Convergence achieved
rand
LEV.  PARAMETER       (NCONV)    ESTIMATE    S. ERROR(U)  PREV. ESTIM     CORR.
-------------------------------------------------------------------------------
 1    CONS     /CONS     ( 1)       14.11          1.743        14.11
 1    CONSD    /CONS     ( 1)       4.028          2.008        4.028
 1    CONSD    /CONSD    ( 2)           0              0            0
fixe
 

  PARAMETER            ESTIMATE     S. ERROR(U)   PREV. ESTIMATE
A2                       0.3722       0.3144             0.3722
D2                      0.08768       0.3247            0.08768
like

-2*log(lh) is      1163.69
fpar 'd2'
sett
EXPLanatory variables in       CONS     CONSD    A2       D2
FPARameters                                      A2
RESPonse variable in           Y
FSDErrors : uncorrected                 RSDErrors : uncorrected
MAXIterations  20   TOLErance     2     METHod is IGLS    BATCh is OFF
IDENtifying codes : 1-ID, 2-CONS

LEVEL 1 RPM
         CONS     CONSD
CONS     1
CONSD    1        1
star

rand
fixe
like
next

Convergence achieved
rand
LEV.  PARAMETER       (NCONV)    ESTIMATE    S. ERROR(U)  PREV. ESTIM     CORR.
-------------------------------------------------------------------------------
 1    CONS     /CONS     ( 1)       14.11          1.743        14.11
 1    CONSD    /CONS     ( 1)       4.038           2.01        4.037
 1    CONSD    /CONSD    ( 2)           0              0            0
fixe
 

  PARAMETER            ESTIMATE     S. ERROR(U)   PREV. ESTIMATE
A2                       0.4562      0.04503             0.4562
like

-2*log(lh) is      1163.76
clrv 1 'consd'
tole 4
maxi 100
sett
EXPLanatory variables in       CONS     CONSD    A2       D2
FPARameters                                      A2
RESPonse variable in           Y
FSDErrors : uncorrected                 RSDErrors : uncorrected
MAXIterations 100   TOLErance     4     METHod is IGLS    BATCh is OFF
IDENtifying codes : 1-ID, 2-CONS

LEVEL 1 RPM
         CONS
CONS     1
star
rand
fixe
like
next

Convergence achieved
rand
LEV.  PARAMETER       (NCONV)    ESTIMATE    S. ERROR(U)  PREV. ESTIM     CORR.
-------------------------------------------------------------------------------
 1    CONS     /CONS     ( 1)       17.05           1.68        17.05
fixe
 

  PARAMETER            ESTIMATE     S. ERROR(U)   PREV. ESTIMATE
A2                       0.4544      0.04836             0.4544
like

-2*log(lh) is      1168.81
stop

The MLn script is as follows. Suppose our MLn command file is anova.ml1, start MLn from network (by typing N:\MLN) and then obey anova.ml1, then you should be able to get the above output. Note the location of data and logo files need be changed.

dinp c1-c8
u:\lecture\genetics\lecture\anova.1
logo u:\lecture\genetics\anova.out
name c1 'ID' c2 'Y' c3 'wgt' c4 'A2' c5 'D2' c6 'C2' c7 'CONS' c8 'CONSD'
resp 'Y'

note weight==.5
iden 1 'id' 2 'cons'
expl 'cons' 'consd' 'a2' 'd2'
fpar 'cons' 'consd'
setv 1 'cons' 'consd'
sett
star
rand
fixe
like
next
rand
fixe
like
fpar 'd2'
sett
star
rand
fixe
like
next
rand
fixe
like
clrv 1 'consd'
tole 4
maxi 100
sett
star
rand
fixe
like
next
rand
fixe
like
stop
 

Example 5.16 Falconer's approximation for MZ and DZ tetrachoric correlations.

MZ A=1.6424560179 RM=0.4644076033
DZ A=1.5928158852 RD=0.2371256092

Example 5.18 The tetrachoric correlations and VA, VD estimates.

RM=0.4883032777  SEM=0.1044075369
RD=0.2483505375  SED=0.3640990882

VA=0.4799054804 SVA=0.7575462488
VC=0.0083977973 SVC=0.7356449672

The thresholds of the liability to have a high neuroticism score (>15) are given by example 5.12, the SAS program for examples 5.16 and 5.18 is as follows.

data _null_;
  n=108;
  t=1.145;
  a=pdf('normal',t,0,1);
  a=a/(1-probnorm(t));
  qm=46/131;
  rm=(t-probit(1-qm))/a;
  sem=(1/(a**2*rm))*sqrt((1-qm)/(qm*n));
  put a= rm= ;
  d=probit(1-qm);
  rm=(t-d*sqrt(1-(t**2-d**2)*(1-t/a)))/(a+d**2*(a-t));
  put rm= sem=;

  n=66;
  t=1.084;
  a=pdf('normal',t,0,1);
  a=a/(1-probnorm(t));
  qd=18/75;
  rd=(t-probit(1-qd))/a;
  sed=(1/(a**2*rd))*sqrt((1-qd)/(qd*n));
  put a= rd= ;
  d=probit(1-qd);
  rd=(t-d*sqrt(1-(t**2-d**2)*(1-t/a)))/(a+d**2*(a-t));
  put rd= sed=;

  va=2*(rm-rd); sva=sqrt(4*(sed**2+sem**2));
  vc=2*rd-rm;   svc=sqrt(4*sed**2+sem**2);
  put va= sva=;
  put vc= svc=;
run;
 

Structural equation models for twin data using Mx 

Example 5.20 Structural equation models for continuous twin data using Mx.

Mx could simply be started with the following ways:

mx
mx  inputfile outputfile
mx <myfile.mx  >myfile.mxo &

Under the first format, the program prompts: Please enter the input filename (Ctrl-c to quit).
The second format is to provide input and output filenames as command line parameters. Usually inputfile and outputfile have extension .mx and .mxo, respetively. The third format start Mx in the background under Unix environment. Under MS Windows, Mx could be setup as short cut; after execution you could open and execute an existing command file.

The script have three things: keywords, parameters and numbers. Keywords must start on a new line. Parameters pass information , e.g. filenames or numbers to commands. Anything after ! is comment. An minimum specifications will include the following commands.

Take the script of the second example from Mx, the observed covariance matrix (COV)  was obtained from 150 observations about three variables,. It tries to establish the factor model COV=AA'+D, where A and D are the factor loading matrix and  unique factor matrix, respectively. Each of them has three unknown parameters.

!
! Anything after a ! is a comment
!
! Mx script to fit a simple model
! One factor in A plus specifics in D
! Use #define to simplify setting matrix dimensions
!

#define nvar 3
#define nfac 1

Simple MX example file
 Ngroups=1
 Data NObservations=150 NInput_vars=nvar
 CMatrix
  1.2
  .8 1.3
  .4 .3 1.4

 Begin Matrices;
  A Full nvar nfac Free
  D Diag nvar nvar Free
 End Matrices;

 Start .5 All                     !  All free parameters to start at .5
 Bound 0 100 D 1 1 to D nvar nvar ! Keep specific variances positive

 Covariance A*A' + D ;

 Option RS ! to get residuals
End

The output from Mx is as follows.

 MATRIX A
 This is a FULL matrix of order    3 by    1
             1
 1      1.0328
 2      0.7746
 3      0.3873
 
 MATRIX D
 This is a DIAGONAL matrix of order    3 by    3
             1          2          3
 1      0.1333
 2      0.0000     0.7000
 3      0.0000     0.0000     1.2500
 
 OBSERVED COVARIANCE MATRIX
             1          2          3
 1      1.2000
 2      0.8000     1.3000
 3      0.4000     0.3000     1.4000
 
 
 EXPECTED COVARIANCE MATRIX
             1          2          3
 1      1.2000
 2      0.8000     1.3000
 3      0.4000     0.3000     1.4000
 
 RESIDUAL MATRIX
               1            2            3
 1   -1.7704E-07
 2   -2.0424E-07  -1.4347E-07
 3   -1.2676E-07   3.5314E-08  -5.2318E-08
 
 Function value of this group:    6.7271E-12
 Where the fit function is Maximum Likelihood
 
 Your model has    6 estimated parameters and      6 Observed statistics

 
 Chi-squared fit of model >>>>>>>     0.000
 Degrees of freedom >>>>>>>>>>>>>         0
 Probability incalculable
 Akaike's Information Criterion >     0.000
 RMSEA >>>>>>>>>>>>>>>>>>>>>>>>>>     0.000

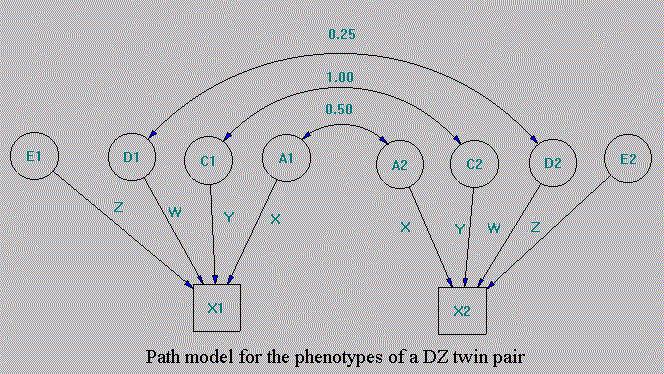
It is a saturated model so the Chi-square fit is zero and none degree of freedom left. Now turn to our neuroticism dataset, we can use MxWin to generate the path diagram (alison.mxd) such as figure 5.5.

The script for ADE model is as follows.

!A D E model fitted to Alison's Data
G1: model parameters
Data Calc NGroups=4
Begin Matrices;
X Lower 1 1 Free    ! genetic structure
Y Lower 1 1 Fixed   ! common environmental structure
Z Lower 1 1 Free    ! specific environmental structure
W Lower 1 1 Free    ! dominance structure
Begin Algebra;
A= X*X' ;
C= Y*Y' ;
E= Z*Z' ;
D= W*W' ;
End Algebra;
End

G2: Monozygotic twin pairs
Data NInput-vars=2 NObservations=522
LAbels N_T1 N_T2
CMatrix
17.64
8.1421 17.64
Matrices= Group 1
COvariances  A+C+D+E | A+C+D _
A+C+D   | A+C+D+E /
Options RSidual SE CI=95
END

G3: Dizygotic twin pairs
Data NInput_vars=2 NObservations=272
LAbels N_T1 N_T2
CMATRIX
18.4599
3.5303 18.4599
MAtrices= GROUP 1
H Full 1 1
Q Full 1 1
Covariances A+C+D+E   | H@A+C+Q@D _
H@A+C+Q@D | A+C+D+E /
MAtrix H .5
MAtrix Q .25
STart .6 ALL
Options Multiple RSidual SE CI=95
End

G4: beta-test
DAta calc
MAtrices= Group 1
compute (A|C|D|E) @ (A+C+D+E)~/
Options RS ND=3 SE CI=95
Options multiple
End

Mx scripts can be split into many groups and allows communication between them, it is thus more flexible than program such as LISREL. The program gives the following estimates.

 EXPECTED MATRIX of this CALCULATION group
           1        2        3        4
 1     0.279    0.000    0.188    0.533
 

Example 5.21 Structural equation model analysis assuming complete ascertainment.

!A D E model fitted to Alison's Data with ascertainment
G1: model parameters
Data Calc NGroups=9
Begin Matrices;
X Lower 1 1 Free    ! genetic structure
Y Lower 1 1 Fixed   ! common environmental structure
Z Lower 1 1 Free    ! specific environmental structure
W Lower 1 1 Free    ! dominance structure
M Full  1 2 Fixed
T Full  2 1 Fixed
V Full  2 1 Free
End Matrices
Matrix T 15.5 15.5
Matrix M 10.23 10.23
! Specify M
! 0 0
Begin Algebra;
A= X*X' ;
C= Y*Y' ;
E= Z*Z' ;
D= W*W' ;
V= T-M' ;
End Algebra;
End

G2: Monozygotic twin pairs
Data NInput-vars=2 NObservations=131
Raw_data file=mz.dat
Labels N_t1 N_t2
Matrices= Group 1
Mean M /
Covariances  A+C+D+E | A+C+D _
             A+C+D   | A+C+D+E /
Options RSidual
End

G3: dummay group
Data Ninput=2
CTable 2 2
0 0
0 0
! It's full of zeros so it contributes zero to the function
Matrices = Group 1
Thresholds V /
Covariances  A+C+D+E | A+C+D _
             A+C+D   | A+C+D+E /
Option RSiduals
End

G4: Calculate ascertainment correction
Data Ninput=0
Matrices
I Iden 1 1
J Izero 1 2
P Full 2 2 = %P3
T Full 1 1
K Unit 2 1
Compute T*\ln(I-J*P*K) /
Matrix T 262                 ! twice the sample size of group 2
Options User-defined RSiduals Multiple
End

G5: Dizygotic twin pairs
Data NInput_vars=2 NObservations=75
Raw_data file=dz.dat
Labels N_t1 N_t2
Matrices= Group 1
H Full 1 1
Q Full 1 1
Mean M /
Covariances A+C+D+E   | H@A+C+Q@D _
            H@A+C+Q@D | A+C+D+E /
Matrix H .5
Matrix Q .25
Start 3.5 All
Options Multiple RSidual
End

G6: dummy group
Data Ninput=2
CTable 2 2
0 0
0 0
! It's full of zeros so it contributes zero to the function
Matrices = Group 1
H Full 1 1
Q Full 1 1
Thresholds V /
Covariances A+C+D+E   | H@A+C+Q@D _
            H@A+C+Q@D | A+C+D+E /
Matrix H .5
Matrix Q .25
Option RSiduals
End

G7: Calculate ascertainment correction
Data Ninput=0
Matrices
I Iden 1 1
J Izero 1 2
P Full 2 2 = %P6
T Full 1 1
K Unit 2 1
Compute T*\ln(I-J*P*K) /
Matrix T 150                 ! twice the sample size of group 5
Options User-defined RSiduals Multiple
End

G8: standardization
data calc
matrices= Group 1
compute (A|C|D|E) @ (A+C+D+E)~/
options rs nd=3
options multiple
end

G9: Constraint group
Data Constraint NInput=1
matrices= Group 1
U Full 1 1
Begin Algebra;
S= (X|Y|W|Z);
End Algebra;
Matrix U 18.0
Constraint U - S*S'/
end

The program gives the following estimates for (A, D, E).

EXPECTED MATRIX of this CALCULATION group
           1        2        3        4
 1     0.295    0.000    0.166    0.539
 
 
The programs allowing for adjustment of ascertainment are given for ADE, ACE, AE, DE, CE, and E models, respectively.
Models with means and variances as free parameters are also given for ADE, ACE, AE, DE, CE and E only.
 

Regressive models and Haseman-Elston sib pair analysis using SAGE 

Chapter 5 does not provide an example for this. Bonney's regressive models and Haseman-Elston sib pair analysis have been sucessfully implemented in the package SAGE (Statistical Analysis for Genetic Epidemiology). It is composed of series of programs and famous for its capability to include covariates in the analysis. Here we introduce programs FSP, REGC and SIBPAL. FSP is a program for family structure processing. REGC is a program for segregation analysis of continuous trait using regressive models. SIBPAL is a program for Haseman-Elston sib pair analysis.

FSP builds a data structure for each pedigree, checks pedigree data for correctness of coding, prepares data for use in SIBPAL and REGC. As of SAGE 2.2, the typical input and output files for FSP, REGC and SIBPAL are listed as follows.
 

Here we set up examples from sage. You can examine these sample files, they are in strict Fortran format. Now you can type name of  the program (eg fsp) at DOS prompt, you can issue exit command to return to Windows. We will not go into more details of these programs. Since Fortran refuses to open an existing file for output, you need delete the previous results in order to run the program again. We have a very naive DOS program clean.bat to do this.

 


This notes is prepared for the genetic course in Institute of Psychiatry during March 3-23, 1998. The major reference is chapter 5 of Sham PC (1998) Statistics in Human Genetics. Arnold.

Any suggestions and problems brought to our attention is appreciated.
 
Pak Chung Sham and Jing Hua Zhao 16/2/1998